本連載は今回の第6回で最後です。連載最後の回は、分散分析を取り上げます。分散分析には、いろいろなデザインがありますが、今回は、二元配置を取り上げます。
結果検討の順番には意味がある
SPSSなどの統計ソフトを使用して分散分析を行うと、主効果、交互作用、単純効果(単純主効果)の検定結果がすべて出力されます。二元配置の場合、検討の順番は次の通りとなります(島田・野口, 2017: 98–99参照)。
最初に交互作用の検定結果を見ます。
▶交互作用が有意ではない場合→各要因の主効果の検定結果を見ます
(2つの要因の効果が独立に従属変数に効果を持つので、それぞれの要因の主効果を見ます。)
▶交互作用が有意である場合ある→単純効果を見ます
(片方の要因の効果の大きさがもう一方の要因の水準ごとに異なっているので、水準ごとの効果の大きさを検定します。)
次の例は尹(2006)から引用したものです。ここでは、授受補助動詞「てくれる」「てもらう」の使用傾向に関して、日本語母語話者(NS)、韓国で学ぶ日本語学習者(JFL)の上位群と下位群、日本国内で学ぶ日本語学習者(JSL)の上位群と下位群の間で差があるかを検証しています。
被験者群、受益動詞の種類(「てくれる」「てもらう」)を要因とする分散分析の結果、被験者群と受益動詞の種類との間に交互作用が有意であった(F(4, 283) = 5.30, p<.01)。そこで、受益動詞の種類の単純主効果を被験者群の水準ごとに検定したところ、JFL下位群・NSでは有意であった(JFL下位群:F(1, 184) = 22.37, p<.01, NS:F(1, 98) = 16.09, p<.01)が、JFL上位群・JSL下位群・下位群注1では有意ではなかった。
尹(2006:124–125)より引用
(注1:尹(2006)では「下位群・下位群」となっていますが、「下位群・上位群」だと思われます。)
上記記述によると、グループにより、「てくれる」と「てもらう」のどちらが正用数が多いかが異なり(交互作用がある)、グループごとに分析したところ、NSは「てもらう」の使用が多く、逆にJFLの下位群は「てくれる」が多かったとのことです。そして、それ以外のJFLの上位群とJSLの上位群・下位群は、「てくれる」と「てもらう」の正用数には差がなかったと報告されています。
この例のようにまず交互作用の検定結果を報告して、その結果により、主効果か単純効果の結果を報告します。ところが、次の報告例のように、交互作用の結果にかかわらず、まず主効果の結果を報告する研究が多いです。次の表は、自己評価アンケートを学期開始時、中間、終了時に行った結果をまとめたものです。その下の文章は、表1の結果を報告するものです。
表1 中国語母語話者とタイ語母語話者の自己評価アンケート結果

分散分析の結果、時期では有意な主効果が見られ、グループ間では主効果は有意ではなかった。また、時期とグループの交互作用は有意であった。交互作用が認められたため、単純主効果の検定を実施したところ、中国語母語グループ、タイ語母語グループとも単純主効果が有意だった。そこで、母語グループごとに多重比較を実施したところ、中国語グループでは、開始時と半ばの時期の得点の間には有意な差はないが、開始時期と半ばの時期よりも終了時の得点の方が有意に高いことがわかり、タイ語グループでは、開始時よりも半ばの時期と終了時の得点が高く、中間時期と終了時の得点に有意な差は認められなかった。時期に関して単純主効果を見ると、開始時期と終了時期では中国語グループの方が高く、中間時期ではタイ語グループの方が高かった。
(本来ならばF値、p値も報告すべきですが、ここは例示であるため省略しました。)
この例では、まず主効果を報告しています。しかし、交互作用があるため主効果の結果よりも単純効果の方が有意味な情報を得ることができます。つまり、時期によってグループ間の差の結果が異なる、ということです。これは主効果では見ることができません。主効果の結果は間違っていないわけですから、報告することが絶対いけないというわけではありませんが、そこにはほとんど意味がないので、報告する必要はないというわけです。
必ず報告しなくてはいけない事項がある
上記の例は、報告しなくてもいい主効果の結果が報告されていた例ですので、大きな問題ではないかもしれません。次にあげるのは、交互作用の結果が記載されていないというものです。「交互作用」が有意かどうかによって、「主効果」を見るか「単純効果」を見るかが決まりますので、「交互作用」の結果は重要です。この「交互作用」の結果が報告されていないのは、分散分析の結果としては誤りとなります。次の例では、主効果しか報告していません。主効果しか報告していないということは、交互作用は有意ではなかったのだろうと想像できますが、やはり交互作用の結果は報告するべきです。
韓国語母語話者と中国語母語話者が、それぞれ2種類の作文(テーマ1、テーマ2)を書いた。すべての作文を日本語教師3名が評価し、その平均値をそれぞれの得点とした。要因Ⅰ「母語」、要因Ⅱ「作文課題」の二元配置の分散分析を行ったところ、母語の主効果は有意であったが(F(1, 23)=14.3, p<.01)、作文課題の主効果は有意ではなかった(F(1, 23)=3.3, ns)。
次の例では、交互作用が報告されていないだけではなく、主効果の結果なのか単純効果の結果なのか明記されていません。
学習者の母語(ヴェトナム語と英語)における指示詞の使用(こ、そ、あ)について二元配置の分散分析を行った結果、ヴェトナム語話者においては「そ」の正答数が、英語話者では「こ」の正答数が、ほかの2つよりも有意に高かった(ヴェトナム語話者:F(2, 232)=14.3, p<.01、英語話者:F(2, 232)=12.0, p<.01)。
さらに、上記の例では、母語グループごとに、3つの指示詞の正答数を比較していますので多重比較を実施していると思われます。しかし、その結果が明記されていません。また、最後のカッコ内の統計結果は、記述がありませんが、単純主効果の結果ではないかと思われます。
報告の仕方として記載が不十分な例を見てきましたが、いずれも、「結論」つまり、どの要因が影響しているのか、どの水準が他の水準よりも平均値が高かったかのみを報告しようとしているようです。これは、主効果と単純効果の違い、交互作用や多重比較の意味が読者にとってわかりにくいと考えて、省略しているのかもしれません。結論だけ報告したいという気持ちもわかります。しかし、統計的手法を使用するのであれば、どのような手法を用いて、どのような結果になったかということは明快に報告しなければなりません。
今回、分散分析を使用している各種論文を読みましたが、どのような分散分析を行っているかわからないものが少なからずありました。原因の1つは、「一元配置」なのか「二元配置」なのかが書かれていないことです。「分散分析を行った」だけではなく、「二元配置の分散分析を行った」と書いた方がわかりやすいと思います。また、平均値や標準偏差を示した表や分散分析表が適切に示されていないことも原因の1つです。少なくとも表1のようなものがあれば、二元配置だということがわかります。t検定の回でも書きましたが、平均値だけではなく、標準偏差も報告する必要があります。
比率の差を検討する場合は要注意
あまり統計の入門書には記載されていないのですが、比率の値をそのまま分散分析で計算するのは正しくありません。これはt検定の式にそのまま比率データを入れて計算することも同じです。
最初にt検定の例として島田(2003)を引用します。この研究は、聴解テストにおいて、選択枝を提示するのに文字で提示した時と音声で提示した時とでは結果が異なるかということを検討したものです。表2にある通り、実験項目数は17で、文字で提示した時の正答率の平均は0.736、音声で提示した時の正答率の平均は0.668です。この間で差があるかt検定を行い、その結果有意差が認められたというものです。ここで検定したのは正答率、つまり、比率の値です。ですから、本来ならば、t検定を行ってはいけません。この時、島田はこのことを知らず、正答率の平均値の差をt検定で検証してしまいました。
表2 聴解テスト選択枝形式による正答率平均の違い
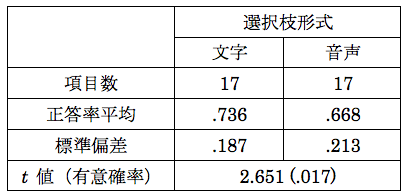 島田(2003)の表6を一部改編
島田(2003)の表6を一部改編
比率の平均の差を検定する場合は、比率の差の検定を使用したり、角変換などを用いて、比率データを変換してから検定にかけたりします。言語教育分野では、比率の平均の差を検討することはあまりありませんが、上記のような正答率の平均や音声的特徴の生起率(例えば無声化の生起率)などが考えられます。日本語教育分野で比率の差の検定を行った例に島田・侯(2009)、角変換を行った例に田中(2005)があります。
比率の値が分散分析やt検定で使用できないわけ
「比率の値は使えませんよ。」と言われただけでは、なかなか納得できないですよね。最後にこの理由について簡単に触れておきます。詳しくはこの連載の程度を大きく超えてしまいますので省略します。
まず、t検定の場合ですが、t検定では「比較する2つの母集団で分散が等しいか否か」によって、用いる方法が違っていました。等分散であることが成り立っている場合には、通常のt検定を用いますが、そうでない場合にはウェルチの方法(島田・野口,2017:54参照)を用います。ところで、比率データをt検定しようとする場合には、比率データの母分散が、母比率×(1-母比率)で表わされるということから、母集団での分散が等しいことを仮定すると、必然的に2つの集団で、「母比率も等しくなる」か「一方の母比率が、他方の(1-母比率)と等しくなる」かのどちらかしかあり得なくなってしまいます(数式を少し展開するとわかるのですが、いまはそんなものか、として先に進んで下さい)。すなわち、母分散が等しいという仮定をおくと、母比率が固定されてしまうことになります。これでは、母分散が等しいとしても、その下で母平均に違いがあるかないかを検討するt検定は使えないですね。
次に、分散分析の場合についてですが、例えば、一要因の分散分析で3水準の場合を考えてみましょう。分散分析では3つの水準で母分散が等しい時に、3つの水準間で母平均が等しいか否かを検定することができます。この場合も比率データでt検定をしようとする場合と同じことが起きてしまいます。この時、角変換(逆正弦変換)と呼ばれる変換(![]() )を比率データに実施するとyの分散の大きさが近似的に標本数のみと関係して、標本数が等しい場合に「等分散性の仮定」が成立します。すなわち、分散分析を実行する前提条件が満たされるわけです。ただし、角変換に関しては、pの値が0または1に近い時に近似があてはまりにくくなる、標本数が水準間で等しくない場合には等分散にならない、などの問題もあります。最近はロジット変換(
)を比率データに実施するとyの分散の大きさが近似的に標本数のみと関係して、標本数が等しい場合に「等分散性の仮定」が成立します。すなわち、分散分析を実行する前提条件が満たされるわけです。ただし、角変換に関しては、pの値が0または1に近い時に近似があてはまりにくくなる、標本数が水準間で等しくない場合には等分散にならない、などの問題もあります。最近はロジット変換(![]() )が用いられることが多くなっています。
)が用いられることが多くなっています。
いずれにせよ、比率データを分析する時には、そうでない場合に比べて注意すべきことが多く、統計法の入門書に出てくる方法をそのまま適用すると誤用になってしまうことがあることを頭に入れておいて下さい。
まとめ
今回の内容をまとめると次のようになります。
1. 二元配置の分散分析の結果を報告するときは、まず、交互作用の検定結果を報告します。次に、交互作用が有意ではない場合は、各要因の主効果の検定結果、交互作用が有意である場合は、単純効果の検定結果を報告します。特に次の点には注意が必要です。
・交互作用の検定結果は必ず報告します。
・主効果の結果か単純効果の結果か明記します。
2. 平均値等をまとめた表や分散分析表を示したほうがわかりやすいです。
3. 比率の差を検討する場合は、分散分析やt検定を使えませんので、違う方法を使います。
今回で「統計で転ばぬ先の杖」の連載は終了となります。6回の連載を通して、日頃論文やレポートを読んで統計に関し気になっていることを整理してみました。これから統計結果を報告しようとしている方にとって、少しでも参考になれば幸いです。
引用文献
島田めぐみ(2003)「日本語聴解テストにおける選択肢提示形式の影響」『日本語教育』119、21-30
島田めぐみ・侯仁鋒(2009)「中国語母語話者を対象とした日本語聴解テストにおける選択肢提示形式の影響」『世界の日本語教育』19号、33-48
島田めぐみ・野口裕之(2017)『日本語教育のためのはじめての統計分析』ひつじ書房
田中信之(2005)「推敲に関する講義が推敲結果に及ぼす効果」『日本語教育』124号、53-62
尹喜貞(2006)「授受補助動詞の習得に日本語能力、及び学習環境が与える影響−韓国人学習者を対象に−」『日本語教育』130号、120-129









